CSS229 Note3 SVM(1)

CS229 Note3 SVM(1)

这篇博文主要内容是

• 支持向量机的引入
• 引入函数间距与几何间距
• 在几何间距基础上定义最优边缘分类器
• 引入拉格朗日对偶性(以解决最优边缘分类器的优化问题)

  符号表示

支持向量机分类器：

$$h_{w,b}(x)=g(w^Tx+b)$$

if$g(z)\geq0$,$g(z)=1$,otherwise,$g(z)=-1$。

函数间距与几何间距(Functional and geometric margins)

函数间距

给定一个训练实例$(x^{(i)},y^{(i)})$，$(w,b)$的函数间距被定义为:

$$\hat{\gamma^{(i)}}=y^{(i)}(w^Tx+b)$$

如果间距大于0，代表预测是正确的，间距的值越大，代表预测正确的置信度越大。

用函数间距来度量分类器的效果有一个特性，如果同时n倍缩放$w$和$b$，由于$g(w^Tx+b)=g(2w^Tx+2b)$，这不会改变$h_{w,b}(x)$的值，其只受符号影响，不受量级影响，通过缩放$w$和$b$，函数间距会被缩放，但是不会对分类器效果有任何有意义的影响，因此用函数间距来度量分类器效果是有缺陷的。直观地看，引入某种归一化条件可能会起作用，例如$||w||_2=1$。
给定一个训练集$S=\{(x^{(i)},y^{(i)});i=1,…,m\}$，训练集的函数间距是所有样本的函数间距中最小的那个。

$$\hat{\gamma}=min_{i=1,...,m}\hat{\gamma^{(i)}}$$

几何间距

决策超平面是$w^Tx+b=0$，那么$w$是与分割超平面垂直的。假设有A点，代表标签$y^{(i)}$=1的输入样本$x^{(i)}$，它到决策边界的距离$\gamma^{(i)}$，用线段AB表示。

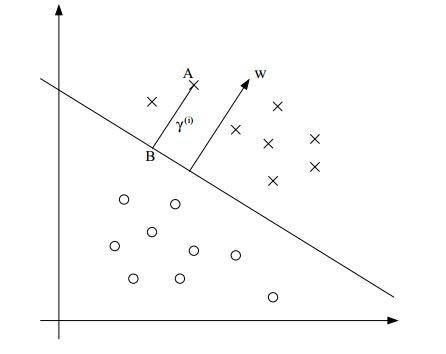
如何得到$\gamma^{(i)}$的值？$w/||w||$是与$w$方向相同的单位向量，由于$A$点用$x^{(i)}$表示，$B$点可以用$x^{(i)}-\gamma^{(i)}.w/||w||$，由于$B$点在决策边界上,有：

$$w^T(x^{(i)}-\gamma^{(i)}\frac{w}{||w||})+b=0$$

从上式可以求得

$$\gamma^{(i)}=\frac{w^Tx^{(i)}+b}{||w||}=(\frac{w}{||w||})^Tx^{(i)}+\frac{b}{||w||}$$

上式是对于正样本的情况，一般的，样本$(x^{(i)},y^{(i)})对$$(w,b)$的几何间距：

$$\gamma^{(i)}=y^{(i)}((\frac{w}{||w||})^Tx^{(i)}+\frac{b}{||w||})$$

如果$||w||=1$，函数间距与几何间距相等。但是几何间距不会受参数的缩放影响，这个特性在之后的推导中是及其有用的，比如我们可以缩放参数来满足某些关于$w$的约束。

最优边缘分类器

给定一个训练集，如何用具有最大几何间距的分类器区分正负样本？

$$max_{\gamma,w,b} \quad \gamma \\ s.t.\quad y^{(i)}(w^Tx^{(i)}+b) \geq\gamma,i=1,...,m \\ ||w||=1.$$

第一个约束条件表示所有样本的函数间距至少是$\gamma$,第二个约束条件确保函数间距与几何间距相等，所以也有几何间距至少是$\gamma$的约束条件。因此，解决该最大化问题可以求得具有最大几何间距的$(w,b)$。
但是$||w||=1$时是一个非凸的问题，不能被优化软件求解，所以需要对优化问题进行变形

$$max_{\gamma,w,b} \quad \frac{\hat{\gamma}}{||w||} \\ s.t.\quad y^{(i)}(w^Tx^{(i)}+b) \geq\hat{\gamma},i=1,...,m$$

现在，最大化的是$\hat{\gamma}/||w||$，约束条件是所有函数间距至少为$\hat{\gamma}$，因为几何间距和函数间距的关系是$\gamma=\hat{\gamma}/||w||$，所以这恰好是我们想要的答案。但是现有软件依旧不能解决这个优化问题，所以需要继续变形。
因为对$w$和$b$进行缩放不会影响决策边界，所以通过缩放$w$和$b$添加约束：训练集的函数间距必须为1。

$$\hat\gamma=1$$

于是问题就变成了最小化$||w||$，等价于

$$min_{\gamma,w,b} \frac{1}{2}||w^2|| \\ s.t. \quad y^{(i)}(w^Tx^{(i)}+b) \geq 1,i=1,...,m$$

现在的问题就变得容易解决了，其结果是一个最优边缘分类器，可以使用二次规划代码来求解。现在，引入拉格朗日对偶(Lagrange duality)，它的主要内容是优化问题的对偶形式，最优边缘分类器在高维空间中能够通过核函数进行有效工作，优化问题的对偶形式有关键作用，另外对偶形式还能推导出一个比一般QP软件更为有效的算法去解决以上的优化问题。

拉格朗日对偶(Lagrange duality)

考虑有以下形式的问题

$$min_w \quad f(w) \\ s.t. \quad h_i(w)=0,i=0,...,l.$$

我们定义拉格朗日函数为

$$\mathcal{L}(w,\beta)=f(w)+\sum_{i=1}^l\beta_ih_i(w)$$

$\beta_i$被称作拉格朗日乘子，通过将$\mathcal{L}$的偏导置为0，可以求解$w$和$\beta$。

原始优化问题

这里的原始优化问题有一个不等式约束和一个等式约束

$$min_w \quad f(w) \\ s.t. g_i(w) \leq 0, i=1,...,k \\ h_i(w) = 0,i =1,...,l.$$

为了解决该问题，定义拉格朗日函数为

$$\mathcal{L}(w,\alpha,\beta)=f(w)+\sum_{i=1}^k\alpha_i g_i(w)+\sum_{i=1}^{l}\beta_i h_i(w)$$

$\alpha_i$与$\beta_i$是拉格朗日乘子
引入如下变量

$$\theta_\mathcal{P}(w)=max_{\alpha,\beta;\alpha_i\geq0}\mathcal{L}(w,\alpha,\beta)$$

$\mathcal{P}$代表”primal”(原始)，如果参数$w$违反了两个约束，易得：

$$\theta_\mathcal{P}(w)=\infty$$

相反，如果参数$w$满足了两个约束,$\theta_\mathcal{P}(w)=\infty$,因此

$$\theta_\mathcal{P}(w)= \begin{cases} f(w), & \text {if $w$ satisfies primal constraints} \\ \infty, & \text{otherwise} \end{cases}$$

因此，当$w$满足约束时，对$\theta_\mathcal{P}(w)$求最小值，就是对$f(w)$求最小值。
所以原始优化问题就可以表示为：

$$min_w\theta_\mathcal{P}(w)=min_w \quad max_{\alpha,\beta;\alpha_i \geq 0}\mathcal{L}(w,\alpha,\beta)$$

即，先把$w$看作常量，求

$$\theta_{\mathcal{P}}(w)=max_{\alpha,\beta;\alpha_i \geq0}\mathcal{L}(w,\alpha,\beta)$$

确定$\alpha$和$\beta$后，原始优化问题的解被定义为$p^{\ast}=min_w\theta_\mathcal{P}(w)$即原始问题的最小最大化。

对偶优化问题

原始问题的对偶问题被定义为

$$\theta_\mathcal{D}(\alpha,\beta)=min_w\mathcal{L}(w,\alpha,\beta)$$

$\mathcal{D}$代表”Dual”，即把$\alpha$与$\beta$看作常量，求最小化$\theta_\mathcal{D}(\alpha,\beta)=min_w\mathcal{L}(w,\alpha,\beta)$确定$w$以后，对偶优化问题被表示为最大最小化

$$max_{\alpha,\beta;\alpha_i\geq0}\theta_\mathcal{D}(\alpha,\beta)=max_{\alpha,\beta;\alpha_i\geq0}\quad min_w\mathcal{L}(w,\alpha.\beta)$$

所以对偶优化问题的解表示为

$$d^*=max_{\alpha,\beta;\alpha_i \geq 0}\theta_\mathcal{D}(\alpha,\beta)$$

原始问题与对偶问题的联系

$$d^{\ast}=max_{\alpha,\beta;\alpha_i \geq 0}\theta_\mathcal{D}(\alpha,\beta) \leq min_w\theta_\mathcal{P}(w) = p^{\ast}$$

在特定条件下，我们有

$$d^{\ast}=p^{\ast}$$

所以可以通过求解对偶优化问题来代替求解原始优化问题。
假设$f$和$g_i$都是凸状的，$h_i$是仿射函数，以及存在$w$使约束$g_i(w) < 0$成立。在以上条件下，一定存在$w^{\ast}$,$\alpha^{\ast}$,$\beta^{\ast}$使$w^{\ast}$是原始优化问题的最优参数，$\alpha^{\ast}$,$\beta^{\ast}$是对偶问题的最优参数，以及$p^{\ast}=d^{\ast}=\mathcal{L}(w^{\ast},\alpha^{\ast},\beta^{\ast})$,此时，$\alpha^{\ast},w^{\ast},\beta^{\ast}$满足以下KKT条件：

$$\frac{\partial}{\partial_{w_i}}\mathcal{L}(w^\ast,\alpha^\ast,\beta^\ast)=0,i=1,...,n \\ \frac{\partial}{\partial_{\beta_i}}\mathcal{L(w^\ast,\alpha^\ast,\beta^\ast)}=0,i=1,...,l \\ a_i^{\ast}g_i(w^{\ast})=0,i=1,...,k \\ g_i(w^{\ast}) \leq 0,i=1,...,k \\ a^{\ast} \geq 0,i=1,...,k$$

$w^{\ast}$,$\alpha^{\ast}$,$\beta^{\ast}$参数满足KKT条件与$w^{\ast}$,$\alpha^{\ast}$,$\beta^{\ast}$是原始问题和对偶问题最优参数互为充要条件。
等式(3)被称为，KKT 对偶互补条件，该式表明如果$a_i^{\ast}>0$,那么$g_i(w^{\ast})=0$,该条件是推导“支持向量机只有少数支持向量”的关键，该条件也对推导SMO算法有极大帮助(convergence test)。